Квадратная и прямоугольная расчетная сетка в FreeFem++

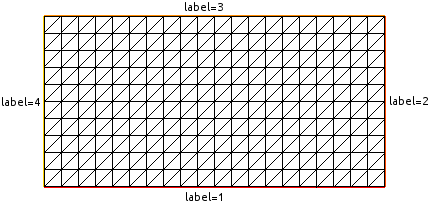
Перейдем к построению расчетной сетки. Простейшим вариантом является команда square создающая квадратную сетку с единичной длиной сторон. Первые два параметра определяют количество сегментов для триангуляции в направлении x и y, соответственно. Для визуализации расчетной сетки используется команда plot. Индексы границ (параметр label) имеют значения от 1 до 4 начиная с нижней границы с нумерацией против часовой стрелки.

mesh Th1 = square(4,6);
plot(Th1);

Для построения прямоугольной сетки задаются третьим и четвертым параметром функции от x и y с координатами соответствующими узлам. Для равномерной прямоугольной сетки размерностью n×m занимающей область [x0, x1]×[y0, y1] можно воспользоваться кодом:

real x0 = 1.2;
real x1 = 2.2;
real y0 = 0;
real y1 = 0.5;
int n = 20;
real m = 10;
mesh Th2 = square(n, m, [x0 + (x1 - x0) * x, y0 + (y1 - y0) * y]);
plot(Th2);

Приямоугольная равномерная расчетная сетка созданная командой square в FreeFem++

Для снижения погрешность расчетов за счет расчетной сетки часто подбирают параметры сетки таким образом, чтобы элементы не имели сильных отклонений по длине ребер, т.е. (x1-x0)/n ≈ (y1-y0)/m.

В задачах, где на различных участках сетки изучаемые переменные меняются в различной степени, точность расчета повышается за счет увеличения размерность сетки. Однако это ведет к увеличению вычислительных ресурсов. Более эффективный способ построения сетки заключается в использовании неравномерных сеток (в области сильного изменения используемой переменной сетка задается более мелкой, а где переменная меняется слабо - более крупной). Для построения неравномерной сетки можно задать нелинейные функции для x и y (диапазон изменения x=0..1 и y=0..1). В следующем примере задается изменение шага для узлов сетки по x и y управляемый параметрами a и b (положительные параметры для уменьшении шага, отрицательные - для увеличения, нулевые - для равномерного шага):

real x0 = 1.2;
real x1 = 2.2;
real y0 = 0;
real y1 = 0.5;
int n = 20;
real m = 10;
real a = 0.3;
real b = 0.2;
mesh Th3 = square(n, m, [x0 + (x1 - x0) * x + a * x * (1. - x), 
                         y0 + (y1 - y0) * y + b * y * (1. - y)]);
plot(Th3);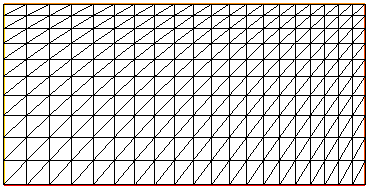

Приямоугольная неравномерная расчетная сетка созданная командой square в FreeFem++

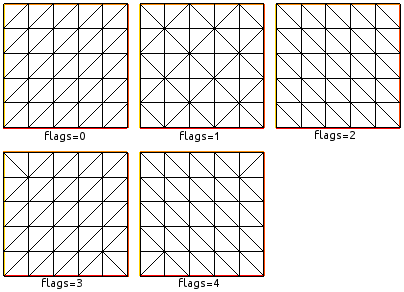
Способ триангуляции задается параметром flags следующим образом:

flags = 0. Создает триангуляцию, где каждый квадрат разделяется диагоналями по закону x - y = const.
flags = 2. Создает триангуляцию, где каждый квадрат разделяется диагоналями по закону x + y = const.
flags = 1. Создает триангуляцию чередующую два предыдущих варианта для нечетных/четных узлов на границе.
flags = 3. То же самое, что и flags = 0, за исключением двух углов, где разбивка делается как для случая flags = 2. Это делается для того, чтобы не было элементов с тремя узлами на границе (и все элементы на границе имели по два узла).
flags = 4. То же самое, что и flags = 2, за исключением двух углов, где разбивка делается как для случая flags = 0. По той же причине, что и для flags = 3.

Пример использования:

mesh Th4 = square(5, 5, flags = 0);

Наглядно примеры триангуляции для различных значений параметра flags видны на рисунке.

Параметр flags для команды square в FreeFem++

Значения индексов границ по умолчанию можно заменить с помощью целочисленного вектора label = lbs. Также можно указать индекс для всей области region (индекс для части объекта, когда логика задачи подразумевает объект из нескольких частей).

int[int] lbs = [0, 0, 1, 1];
mesh Th5 = square(5, 5, flags = 1, label = lbs, region = 2);
plot(Th5);