Построение геометрии объекта в FreeFem++

Область моделирования определяется с помощью границ, заданных параметрически. Граница определяется типом данных border с указанием имени переменной для параметра, и двумя параметрическими уравнениями в декартовых координатах (переменные x, y и z являются зарезервированными и соответствуют координатам). С помощью зарезервированной переменной label можно присвоить индекс границы (в дальнейшем, по индексу задаются граничные условия); если индекс не задан, то устанавливается значение по умолчанию равное 0. Например, зададим границу b1 от точки (0, 0) до точки (0, 0.5) с индексом 1 (параметр t):

border b1(t = 0., 1.) {x = t; y = 0.5 * t; label = 1;}

Для проверки, можно сразу же посмотреть результат в графическом окне с помощью команды plot, в качестве аргумента которой имя переменной типа border с указанием количества сегментов на этой границе (по этим сегментам, позже, строятся конечные элементы, в примере указано 10 сегментов).

plot(b1(10));

Можно вывести одновременно несколько границ, например, чтобы убедится, что они составляют правильную геометрию. Для этого, в команде plot используется объединение нескольких границ (оператор "+").

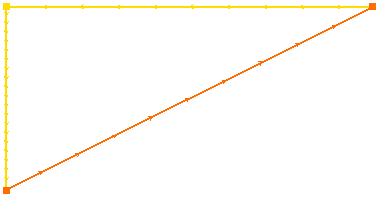
Из примера видно, что геометрия замкнутая (расчетная сетка создается только для замкнутых границ); одна граница относится к одному типу (b1 имеет индекс 1, обозначена оранжевым), а две другие к другому (b2 и b3 имеют индекс 2, обозначены желтым). Стрелками указано направление границ, а количество сегментов определяется количеством стрелок на соответствующей границе.

При определении границы можно использовать внутренние переменные, которые будут определены только внутри описания границы. Например, для определения границы в виде окружности можно использовать дополнительную переменную для аргумента тригонометрических функций (как в первой строке; данный вариант указан в качестве примера, конечно логичнее использовать вариант во второй строке; оба варианта эквивалентны):

border b4(t=0., 1.){real tt=2.*pi*t; x=cos(tt); y=sin(tt);}
border b5(t=0., 2.*pi){x=cos(t); y=sin(t);}

Границу можно задать с помощью двух векторов, содержащие координаты точек границы. Диапазон параметра задается переменной целого типа от нуля (первая координата в векторе) до количества элементов в векторе (последняя координата для вектора vX имеет номер vX.n-1); координаты границы соединяются линиями по координатам заданным векторами через зарезервированную переменную для узлов P (с координатами P.x и P.y).

real[int] vX(4), vY(4);
vX = [0. , 1., 0., 0.];
vY = [0., 0.5, 0.5, 0.];
border b6(t=0, vX.n-1){P.x=vX[t]; P.y=vY[t];}

Конечно, можно расширить последний пример целочисленным вектором для задания индексов границ:

real[int] vX(4), vY(4);
int[int] vL(4);
vX = [0. , 1., 0., 0.];
vY = [0., 0.5, 0.5, 0.];
vL = [1, 1, 2, 2];
border b6(t=0, vX.n-1){P.x=vX[t]; P.y=vY[t]; label = vL[t];}
plot(b6(100));

Поскольку границы задается не через сегменты, а через узлы, то разумно проверить правильность индексации границ визуально командой plot.