Конвекция Рэлея-Бенара
Конвекция Рэлея-Бенара описывается системой уравнений в приближении Буссинеска, состоящее из уравнения Навье-Стокса, уравнения теплопроводности и условия несжимаемости жидкости. Эффект тепловой конвекции проявляется в результате зависимости плотности жидкости или газа ρ от температуры T в объемной силе входящей в уравнение Навь-Стокса (но в конвективном слагаемом плотность считается постоянной).
- ,
- ,
- ,
где ρ0 – плотность при температуре T0, v – скорость, p – давление, μ – коэффициент динамической вязкости, g – ускорение свободного падения, T – отклонение от температуры T0, χ – коэффициент температуропроводности.
При линейной зависимости плотности от температуры ρ(T) = ρ0 (1 - β T), где β – коэффициент объемного расширения, подстановкой давления p1=p-ρ0gy уравнение Навье-Стокса запишется в виде
Подготовка модели в Salome
Для начала нужно создать поверхность размерами 0.06×0.01 (рис. 1).

Рис. 1: Геометрия
Создаем равномерную прямоугольную сетку (рис. 2).

Рис. 2: Расчетная сетка
Моделирование в Elmer
Настраиваем параметры расчетов:
Simulation type = Transient
BDF order = 2
Timestep intervals = 200
Timestep sizes = 2
Добавляем свойства материала
General → Reference Temperature = 293
Объемные силы:
Начальные условия:
Heat equation → Temperature = 293
Navier-Stokes → Velocity 1 = 1.0E-9; Velocity 2 = 0
Граничные условия (нижняя граница):
Heat equation → Temperature = 293.5
Navier-Stokes → Velocity 1 = 0; Velocity 2 = 0
Граничные условия (верхняя граница):
Heat equation → Temperature = 293
Navier-Stokes → Velocity 1 = 0; Velocity 2 = 0
Граничные условия (боковые границы):
Navier-Stokes → Velocity 1 = 0; Velocity 2 = 0
Создаем sif-файл, сохраняем проект и запускаем расчет:
File &rarr Save project
Run → Start solver
Результаты моделирования
Запускаем постпроцессор

Рис. 3: Распределение давления
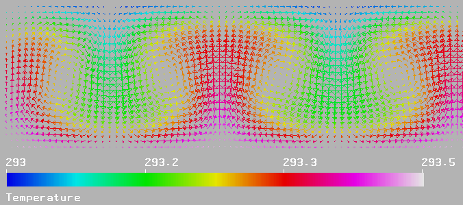
Рис. 4: Векторное поле скорости, цветом обозначена температура
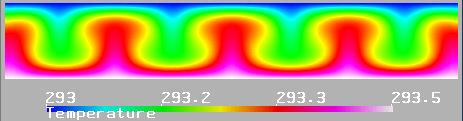
Рис. 5: Распределение температуры
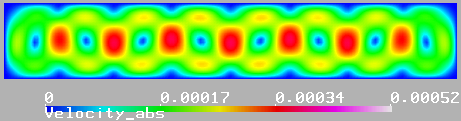
Рис. 6: Распределение модуля скорости